本文不涉及到任何押题,漏题部分,只为同学们分析下近些年压轴题考查内容,同学们针对自己的情况,查缺补漏,力争考的都会,取得好成绩。本人水平有限,还请老师和同学们指正。
济南中考数最近的一次改革从2018年开始,从原有的满分120分提升到150,具体为选择题从15道减为12道,解答题数量表面有所提升,从之前的7道变为9道(18年前的计算和证明题每道题都有两小题)。总的来说就是题变少了,最后几道大题的赋分变多了,对证明、计算过程的要求严格了。

从考查内容来说,改革后也有了一些较大的改变。题型方面相对僵化,改革前虽然有这个趋势,但还不明显,谁也猜不到后三道题考什么,但从14年以后,后三道大题基本都保持着围绕反比例函数、动态几何和二次函数出题。甚至改革后,圆单独出大题,最后三道大题和圆的结合部分也看不到了(要平衡知识点在考试中的比例)。基础题部分的变化相信同学们经历了几个月的模考,已经烂熟于胸了,这里就不多说了。
2020年和2021年在解答题上也做出了一些小变动,22题统计题的最后一问不再考查概率的计算问题,24题的应用题第二问加入了不等式、一次函数求极值的问题,难度略有增加。但对于目标是140分的同学来说,这都不是事。可以这样说,随着老师们复习的系统化,对于题目模型研究的深入,实际上题目的难度要比多年以前有所增加,但另一个问题也随之出现,中考数学后三题还有没有新考法了?
我们来看一下近年来中考中档题和难题都考些什么内容吧。
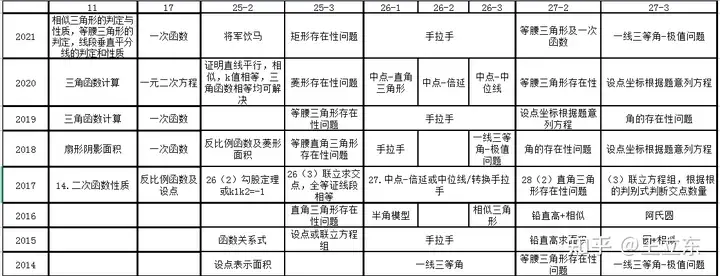
上图列出了选择填空的倒数第二题及后三道大题考查的知识点(为什么没有写选择填空压轴题的知识点?因为那是要拿150分的同学才需要重点考虑的。)这个图的知识点是个人总结的,因为一题多解的原因以及归纳总结的原因,知识点可能和偏差,但我们要从这上面找到一些常考的知识点。
一、图形存在性问题。
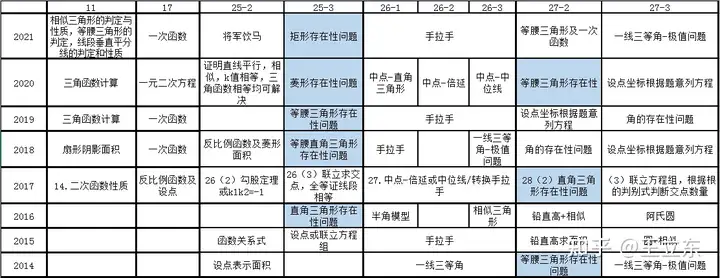
这一类题几乎每年都会考,15年没考图形存在性,但考了个点存在性的问题,暂不去管,我们来看看这些存在性问题的解决方法各位同学你都掌握了吗?

如果你能看懂解题策略并能够想起对应的题目的解法(比如等腰三角形存在性问题中,策略是两圆一线,那么一线上这个点一般来说如何求坐标?想出答案再往下看。答案在本段末尾),恭喜你,这四分应该是稳了。如果你觉得解题策略有地方看不懂我在说些什么,那就得好好赶紧复习一下,从概率上来说,考存在性这是个必然事件呀。(答案是用k1k2=-1和中点坐标公式或者勾股定理解决,如果没想到那就是还不如熟练)
从这些年出题规律上来看,该考正方形存在性了,从重要程度上来说,初中数学里最重要的几何图形是等腰三角形和直角三角形。
小提示:
1、相似三角形的存在性问题也很重要,策略是先判断用两角还是两边夹角判定相似,文字相似(就是问题中出现“∽”还是文字“相似”)必有分类讨论。12年中考压轴题曾经考过这类题,难度相对较大,这里就不讨论了。
2、等腰三角形和直角三角形存在性问题一般要分三种情况讨论,而这类一般出现在中考题25-3,这个题位置属于中档题,所以一般都会通过一定的条件减少一种讨论情况来简化题目,要仔细审题。具体如下图



二、手拉手相似,手拉手全等
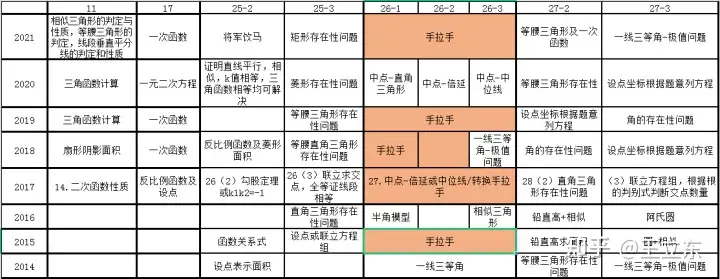
先说干货,手拉手相似、全等的四个结论,以2011年中考最后一题为例:
1、△ACE≌△DCB(SAS) 这里利用边角边证明全等,剩下没有用到的那条边称之为第三边
2、AE=DB 第三边相等
3、∠APD=∠ACD=∠BCE 两条第三边的夹角(可能有锐角和钝角之分)等于拉手点的两个顶角的度数
4、PC平分∠APB 第三边的交点连接拉手点是角平分线(手拉手相似不适用)
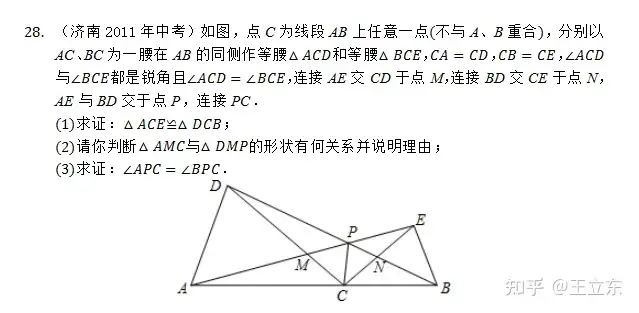
你知道这四个结论,做题的时候就属于站在巨人肩膀上的那一类同学了。当然手拉手还有一些变形,比如脚蹬脚等,具体就不展开讲了。上面这个题是2011年济南中考最后一题,很简单吧?但到了这几年就变画风了,我们来欣赏一下驯化的手拉手。
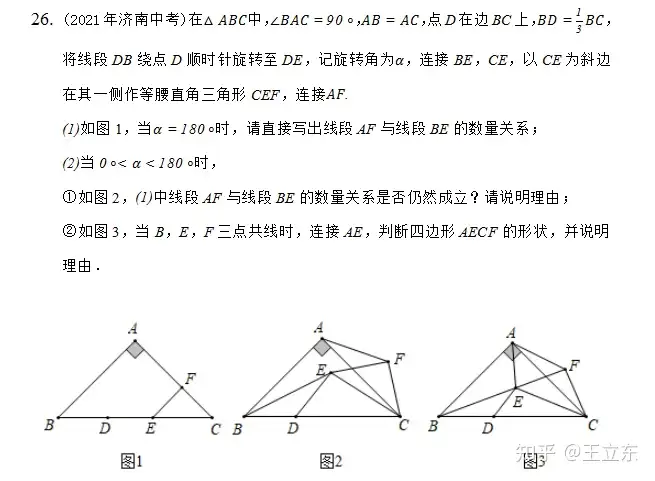
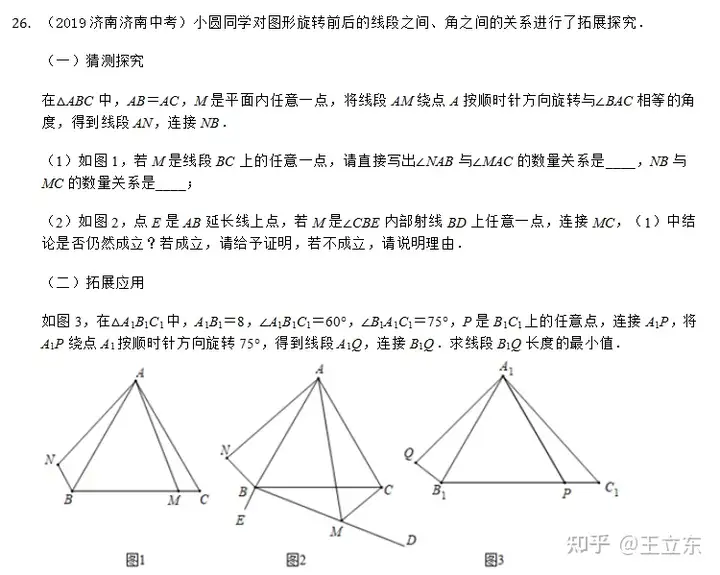
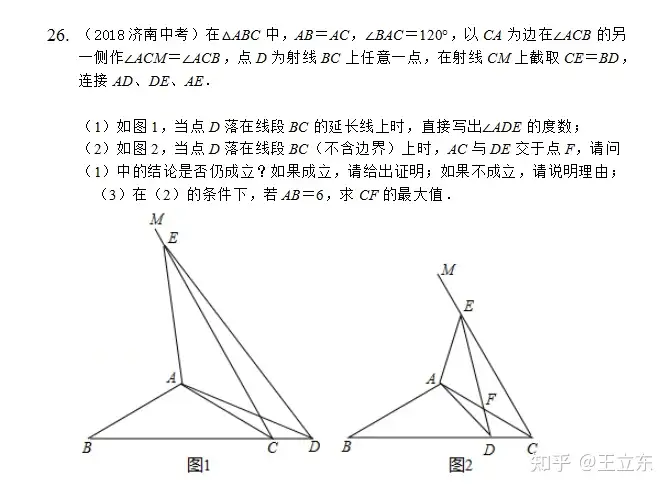
为什么手拉手考的这么频繁?初中的几何图形变换学的是平移和旋转么。旋转这部分能够整理成模型的也就是手拉手,半角模型和奔驰模型等。半角模型(16年考过)和奔驰模型变换形式一个比一个少,你说怎么办?
我也是很期待今年的26题,看看到底是出手拉手,半角模型还是中点问题呀。
三、你知道中点的四种用法吗?
先来干货部分,考试大题中,碰到给了中点又没有给线段长度的,那就从这四个方面去考虑:
1、先观察中点是不是等腰三角形底边的中点
2、再观察中点是不是直角三角形斜边上的中点
3、有没有第二个中点或者能否构造中点形成中位线
4、倍延过中点的另一条线段,构造三角形全等,然后将对应线段再次构造全等寻找题目结论。

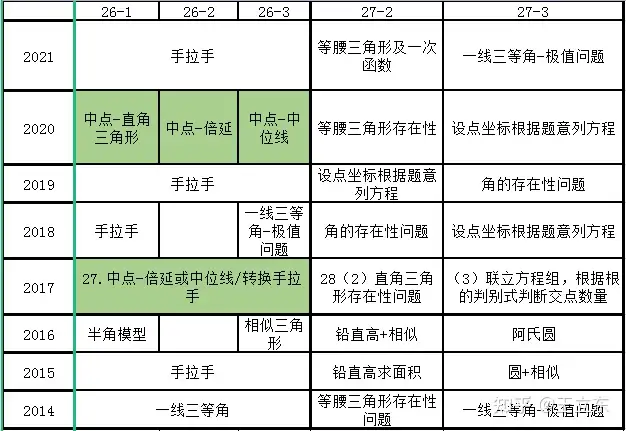
除了手拉手就是中点问题了。直接上原题,自己过一遍思路。
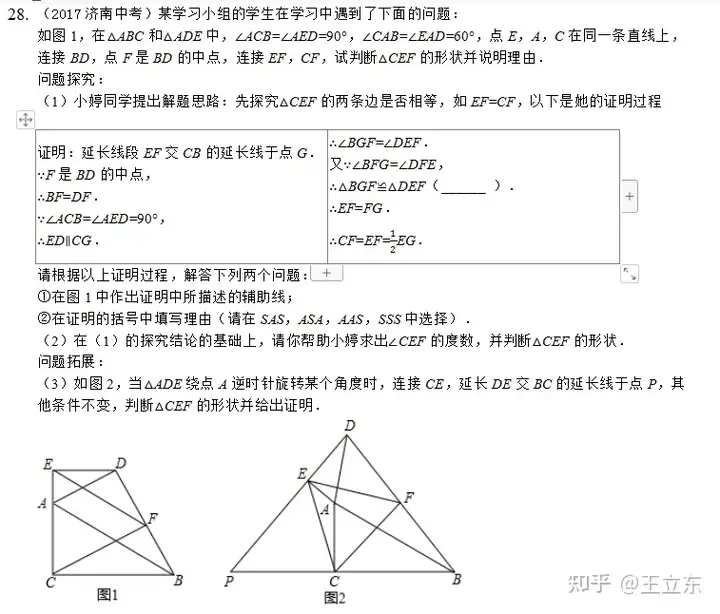
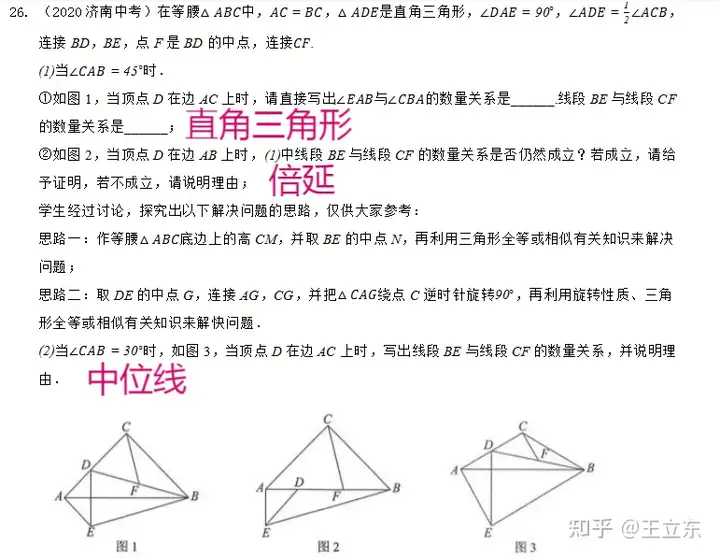
小提示:
1、倍延和中位线要结合考虑,大多数题目,能倍延的也能用中位线去解决。
2、构造倍延后的第二次全等图形一般需要做辅助线去寻找,要注意时间安排,思维要灵活,寻找题目中的相等线段,如果是利用相似的话要从比例线段着手去构造。
3、见到等腰三角形要想到构造三线合一,见到直角三角形要想到30°角所对的直角边等于斜边的一般,还有直角三角形斜边上的中线等于斜边的一半这两个定理。
四、角度存在性问题
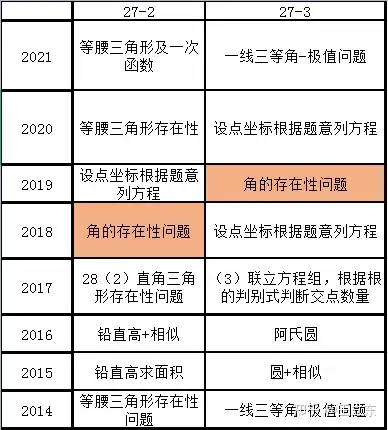
干货:

小提示:
1、12345模型:正切值为1/2和1/3的两个角的和为45°
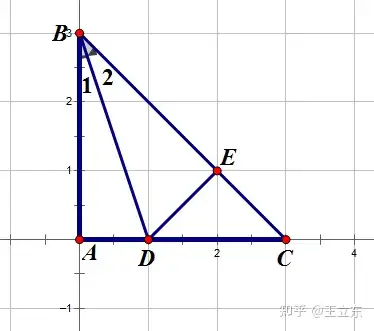
2、12345模型会了的话,进阶版的就要学点高中的知识了:两角正切的和差公式。
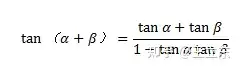
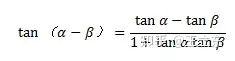
可以将tanα=1/2,tanβ=1/3带入第一个公式,看看tan(α+β)是多少?
可以通过第二个公式求一下tan∠1是多少。
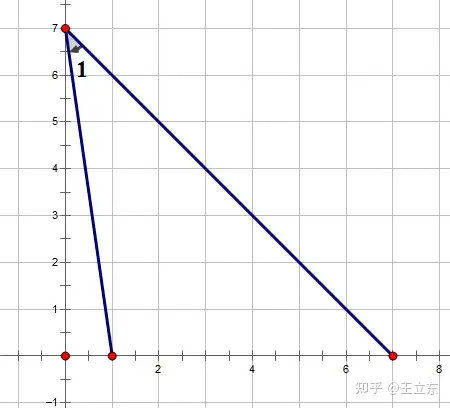
如果你又恰好知道一次函数y=kx+b(k \ne 0)中的 \left| k\right| 等于一次函数和x轴夹角的正切值,那你碰到角度的题将无往不利。


等于一次函数和x轴夹角的正切值,那你碰到角度的题将无往不胜。
五、铅垂高
几乎每次初三上学期期末解答题最后一题都会考一个铅垂高的问题。在中考里铅垂高从来不这么轻易出现,这一问总是要抽丝剥茧才能发现这个题求的是铅垂高。设点,带入解析式,求出铅垂高的二次函数关系式,利用极值解决问题或根据题意列出方程就是这类题的解法。有道是:铅垂高不难,难的是你有没有一双发现它的眼睛。


好几年没考了,你猜今年考不考?
六、我们那个年代初中数学学两门,其中一门叫代数

以前初中数学学两本书,一本叫几何,上课要带圆规,另一本叫代数,里面到处都是英文字母。
现在统一叫数学了,但内容还是那些,学了三年代数了,不得考考你呀?你要学会设一个点的横坐标为m,然后用这个m表示出纵坐标,还能用这个m表示出线段的长度,一次函数的解析式,和直线或坐标轴的交点坐标,最后根据题意列出个关于m的方程,这个m就可以求出具体的值了。难倒不难,需要你有勇气带着m写下去。



七、一线三等角(它有很多名字,k型相似,M型相似等等)
干货
1、碰到直角斜放要学会构造一线三等角
2、动点D为底边中点时,或者EF平行AC时都会使三个三角形都相似。
3、当D为AC中点时,因为相似,可得∠1=∠2,所以点D向EF和CF分别作垂,两条垂线相等,前者不好求,后者很好求。
4、极值问题,一般设要求得值为y,动点路程为x,根据相似列出比例式,然后转化为二次函数,在定义域内求极值即可。



八、还有不少模型,但时间有限,就说这么多吧,最后补充几个常用公式。不熟练就别用,熟练了再用才有用。
1、点到直线的距离公式,

2、一次函数速求k值
已知A(x,y),B(a,b),则直线AB的k=(x-a)/(y-b)
不用解方程组了对不对?
3、顶点在原点的三角形面积的平面向量求法

如题,A(2,4),B(6,1),则面积口算可得11,适用于选择题空题,解答题当做验算最好。
成文较为仓促,难免错字疏漏,还请指出。最后祝各位同学中考顺利,考出自己的水平。
随时根据老师和同学们的口述更新2022年中考原题
2022年中考题






(1)t=3,k=-1/4
(2)(10,-2/7) 直角三角形存在性策略可解
(3)169/16 利用正切和差公式可得切线解析式,联立直线BC即可。还可以设点用含m的代数式表示出相关对应线段,根据二次函数求极值



 陕公网安备 61011302001522号
陕公网安备 61011302001522号